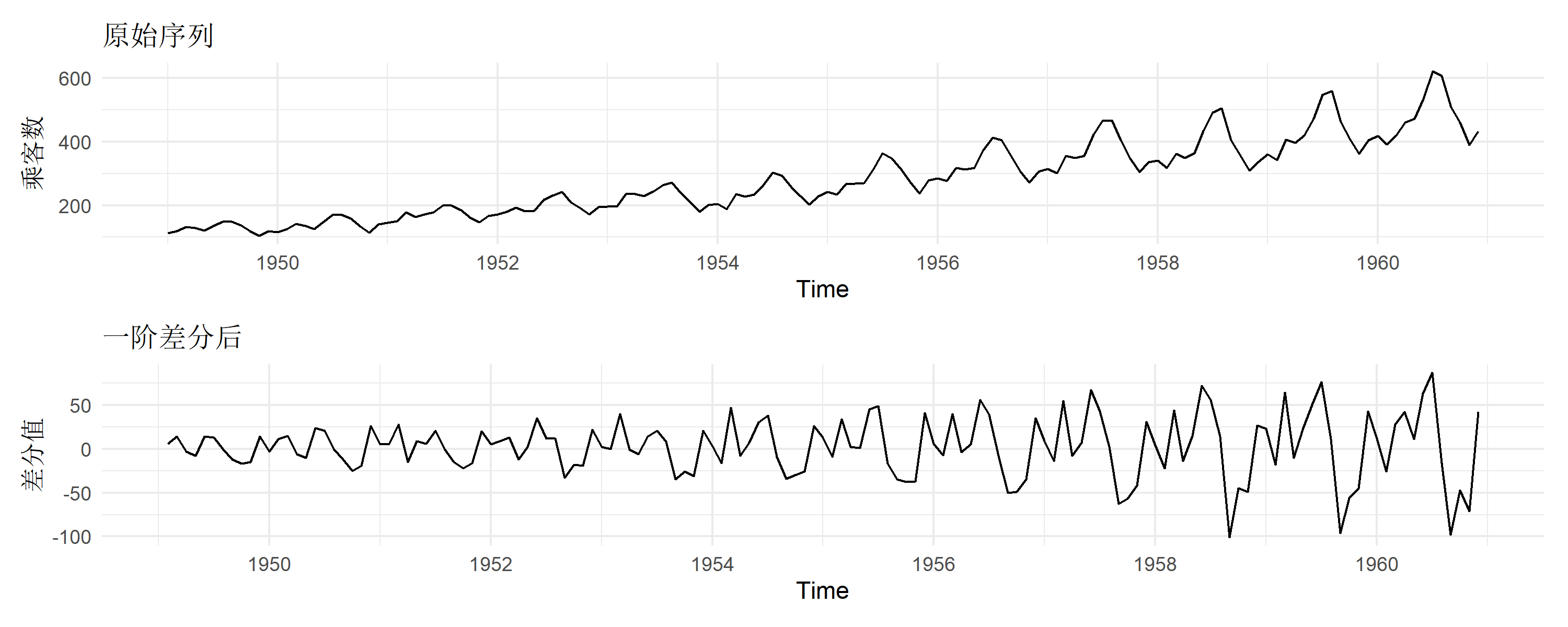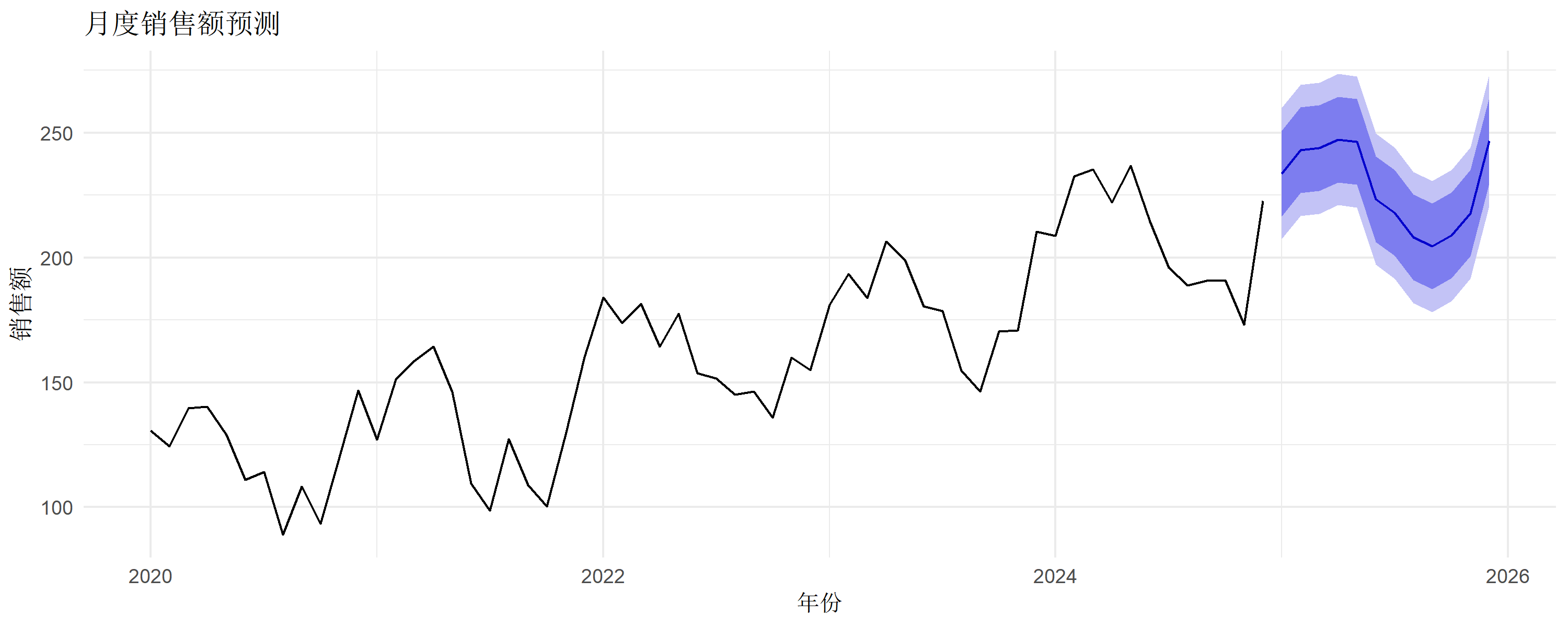时间序列分析

R语言方法
时间序列
预测
Published

January 10, 2025

时间序列分析是研究按时间顺序排列的数据规律的方法，广泛应用于经济预测、气象分析、销售预估等领域。

基础概念

library(forecast)   # 时间序列预测核心包
library(ggplot2)
library(patchwork)

# 使用经典航空乘客数据
data <- AirPassengers  # 1949-1960年月度乘客数（千人）
data
     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
1952 171 180 193 181 183 218 230 242 209 191 172 194
1953 196 196 236 235 229 243 264 272 237 211 180 201
1954 204 188 235 227 234 264 302 293 259 229 203 229
1955 242 233 267 269 270 315 364 347 312 274 237 278
1956 284 277 317 313 318 374 413 405 355 306 271 306
1957 315 301 356 348 355 422 465 467 404 347 305 336
1958 340 318 362 348 363 435 491 505 404 359 310 337
1959 360 342 406 396 420 472 548 559 463 407 362 405
1960 417 391 419 461 472 535 622 606 508 461 390 432

时间序列的三个核心成分：

  • 趋势 (Trend)：长期上升或下降的模式
  • 季节性 (Seasonality)：固定周期的重复波动
  • 残差 (Residual)：去除趋势和季节性后的随机成分

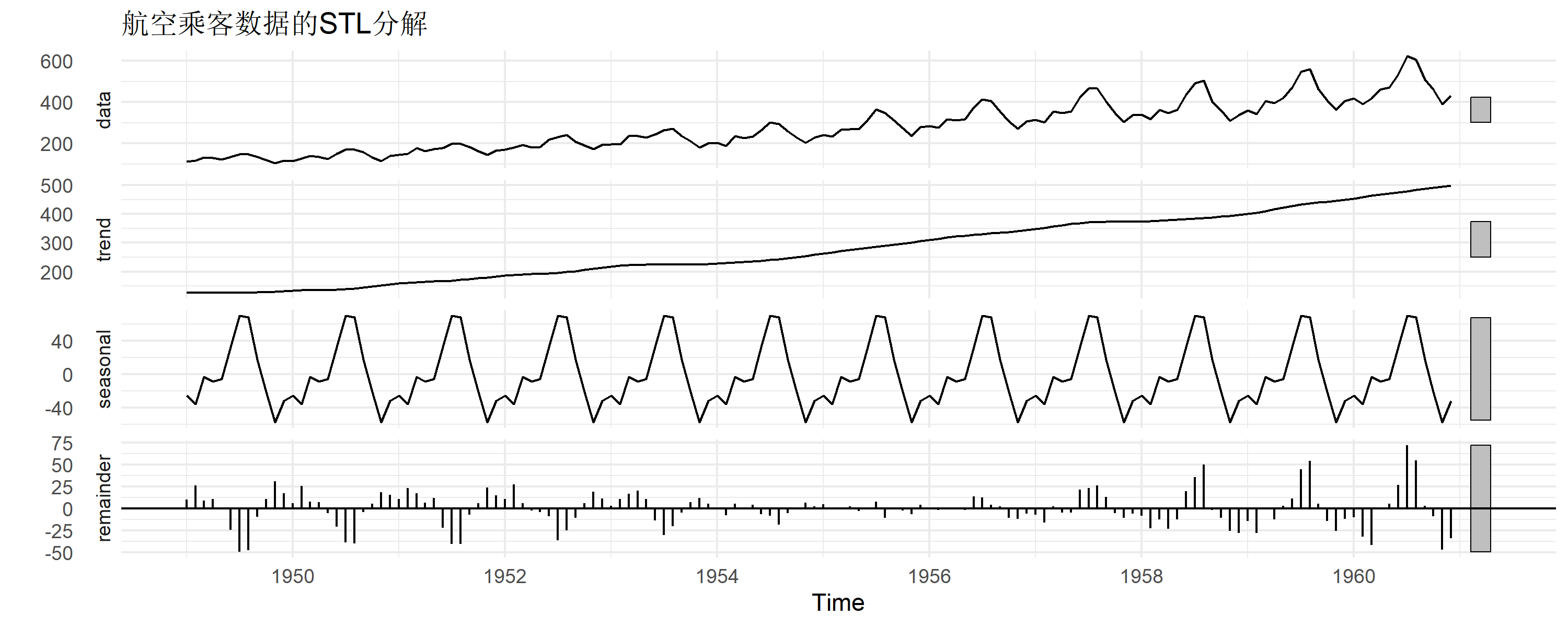
时序分解

将时间序列分解为趋势、季节和残差三部分：

# STL分解：更灵活的现代方法
stl(data, s.window = "periodic") |> 
  autoplot() + 
  theme_minimal() +
  labs(title = "航空乘客数据的STL分解")

Tip

分解类型选择：

  • 加法模型：\(Y = T + S + R\)（波动幅度稳定）
  • 乘法模型：\(Y = T \times S \times R\)（波动随趋势增大，如本例）

平稳性检验

ARIMA模型要求序列平稳。使用ADF检验判断：

library(tseries)

# 原始序列：非平稳
adf.test(data)  # p > 0.05 → 非平稳

    Augmented Dickey-Fuller Test

data:  data
Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01
alternative hypothesis: stationary
# 一阶差分后：平稳
adf.test(diff(data))  # p < 0.05 → 平稳

    Augmented Dickey-Fuller Test

data:  diff(data)
Dickey-Fuller = -7.0177, Lag order = 5, p-value = 0.01
alternative hypothesis: stationary

差分可消除趋势，使序列平稳：

# 对比原始与差分后的序列
p1 <- autoplot(data) + labs(title = "原始序列", y = "乘客数")
p2 <- autoplot(diff(data)) + labs(title = "一阶差分后", y = "差分值")
p1 / p2 & theme_minimal()

ARIMA模型

ARIMA(p,d,q) 是最常用的时间序列模型：

  • p：自回归阶数（AR）
  • d：差分次数
  • q：移动平均阶数（MA）
# 自动选择最优参数（基于AIC准则）
fit <- auto.arima(data)
fit
Series: data 
ARIMA(2,1,1)(0,1,0)[12] 

Coefficients:
         ar1     ar2      ma1
      0.5960  0.2143  -0.9819
s.e.  0.0888  0.0880   0.0292

sigma^2 = 132.3:  log likelihood = -504.92
AIC=1017.85   AICc=1018.17   BIC=1029.35

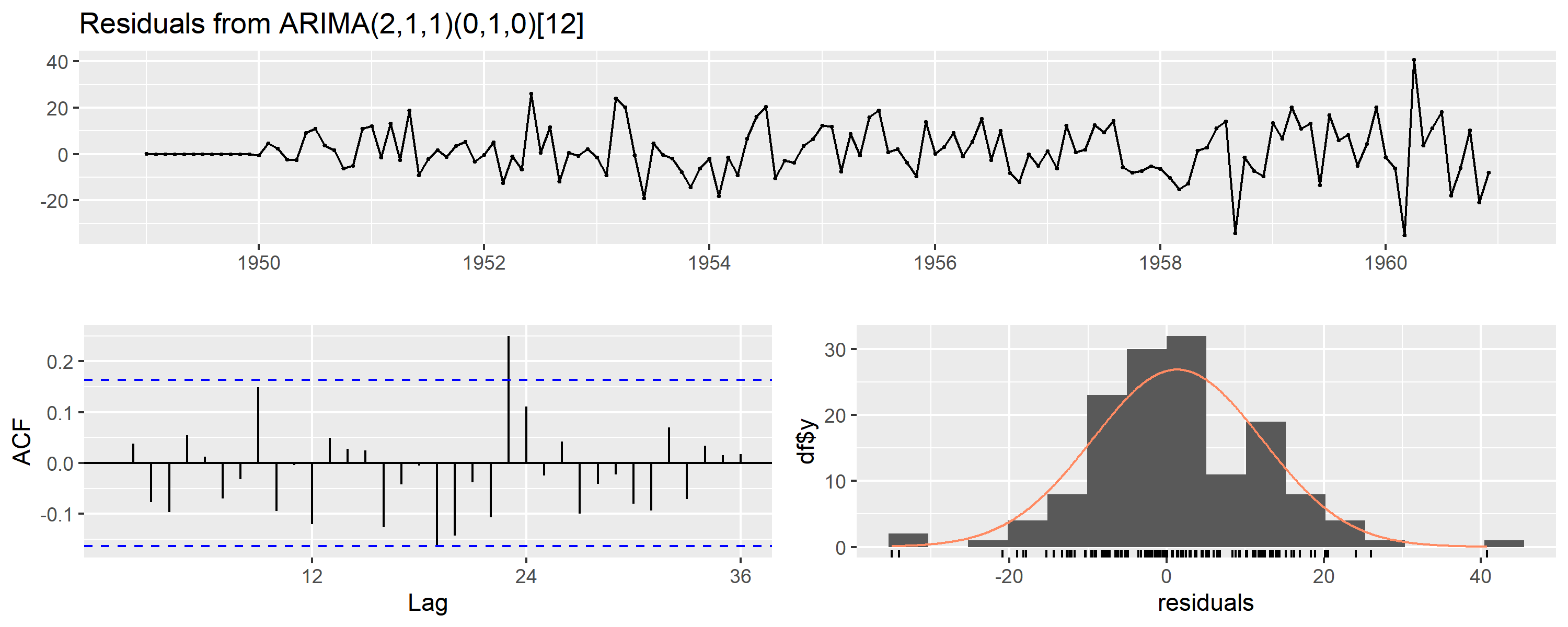
模型诊断

检查残差是否为白噪声：

checkresiduals(fit)  # 残差应无自相关、近似正态


    Ljung-Box test

data:  Residuals from ARIMA(2,1,1)(0,1,0)[12]
Q* = 37.784, df = 21, p-value = 0.01366

Model df: 3.   Total lags used: 24

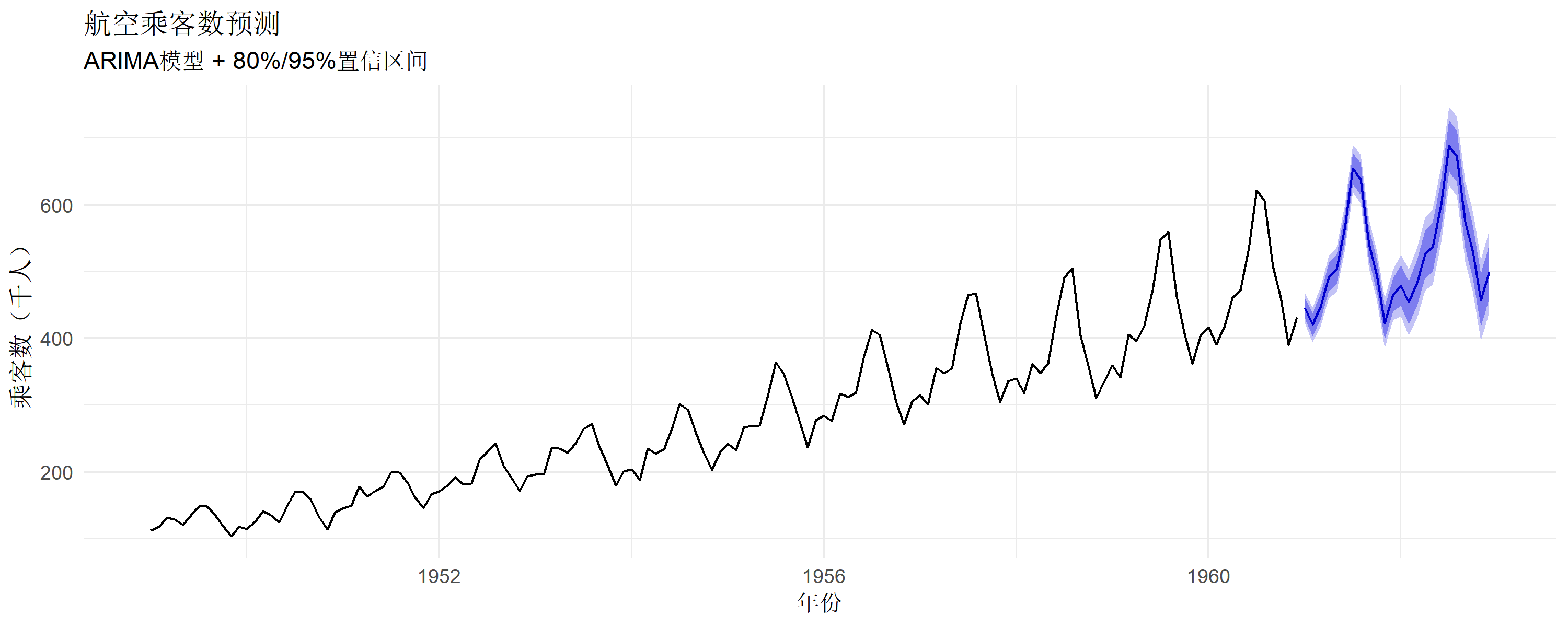
预测

使用拟合模型进行未来预测：

# 预测未来2年（24个月）
fc <- forecast(fit, h = 24)

# 可视化：蓝色区域为置信区间
autoplot(fc) +
  theme_minimal() +
  labs(title = "航空乘客数预测", 
       subtitle = "ARIMA模型 + 80%/95%置信区间",
       x = "年份", y = "乘客数（千人）")

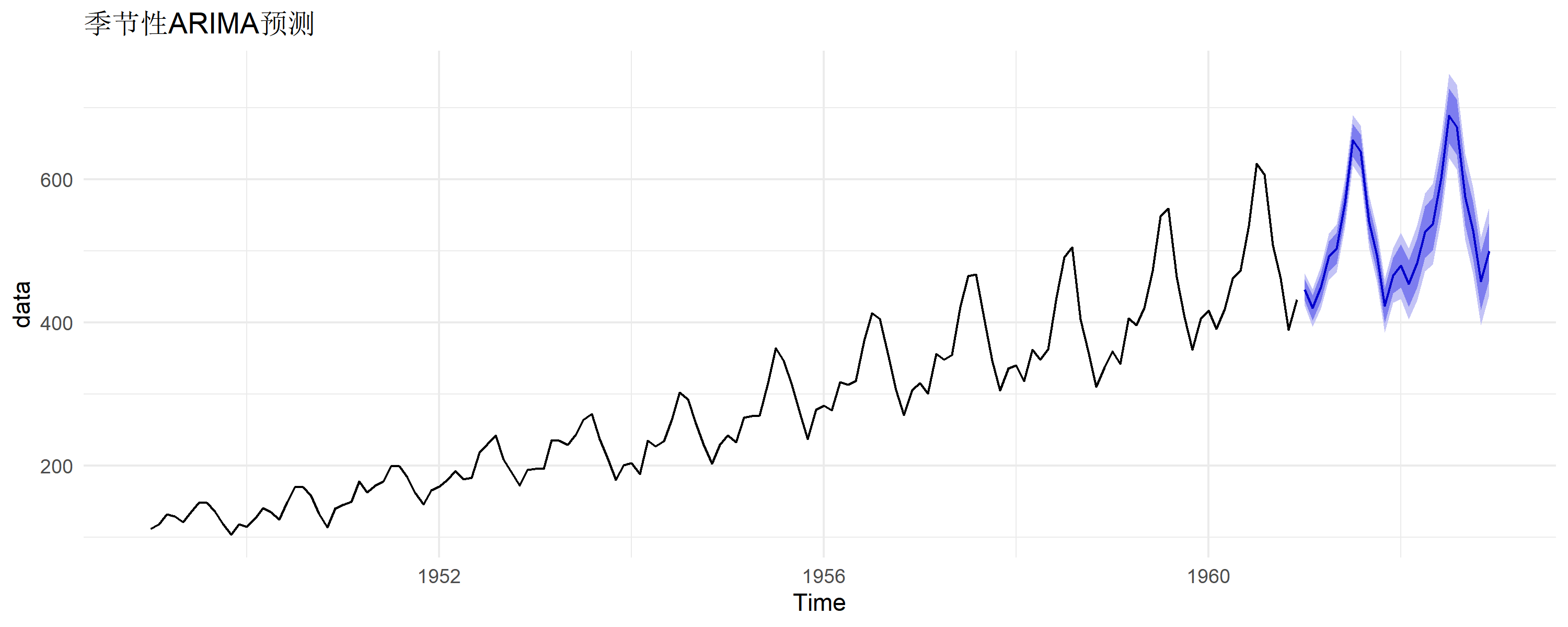
季节性ARIMA

对于有明显季节模式的数据，使用SARIMA：

# 强制使用季节性模型
fit_seasonal <- auto.arima(data, seasonal = TRUE, D = 1)
fit_seasonal
Series: data 
ARIMA(2,1,1)(0,1,0)[12] 

Coefficients:
         ar1     ar2      ma1
      0.5960  0.2143  -0.9819
s.e.  0.0888  0.0880   0.0292

sigma^2 = 132.3:  log likelihood = -504.92
AIC=1017.85   AICc=1018.17   BIC=1029.35
# 预测并对比
forecast(fit_seasonal, h = 24) |> 
  autoplot() +
  theme_minimal() +
  labs(title = "季节性ARIMA预测")

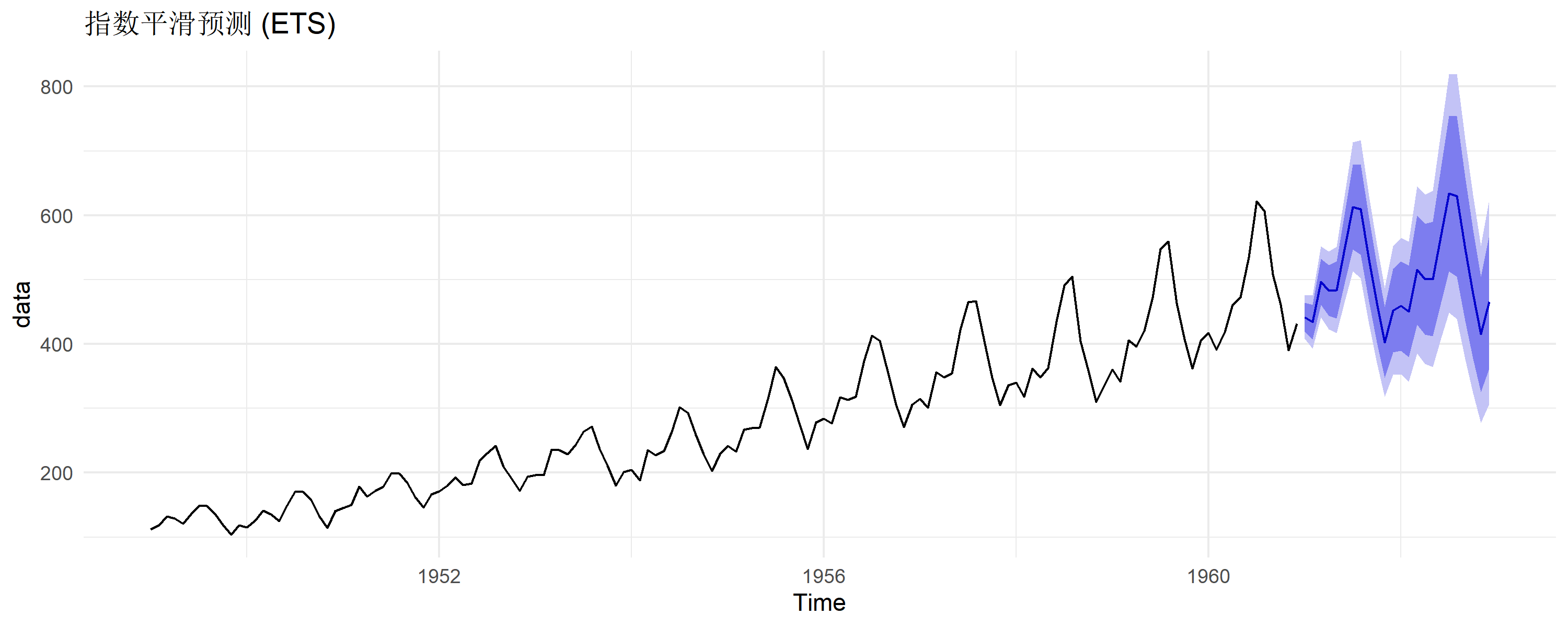
指数平滑法

另一类常用方法，适合短期预测：

# ETS自动选择最优平滑参数
ets_fit <- ets(data)
ets_fit  # M,A,M = 乘法误差、加法趋势、乘法季节
ETS(M,Ad,M) 

Call:
ets(y = data)

  Smoothing parameters:
    alpha = 0.7096 
    beta  = 0.0204 
    gamma = 1e-04 
    phi   = 0.98 

  Initial states:
    l = 120.9939 
    b = 1.7705 
    s = 0.8944 0.7993 0.9217 1.0592 1.2203 1.2318
           1.1105 0.9786 0.9804 1.011 0.8869 0.9059

  sigma:  0.0392

     AIC     AICc      BIC 
1395.166 1400.638 1448.623 
# 预测
forecast(ets_fit, h = 24) |> 
  autoplot() +
  theme_minimal() +
  labs(title = "指数平滑预测 (ETS)")

模型对比

使用交叉验证比较预测准确性：

# 取最后2年作为测试集
train <- window(data, end = c(1958, 12))
test <- window(data, start = c(1959, 1))

# 训练两个模型
m1 <- auto.arima(train)
m2 <- ets(train)

# 预测并计算误差
fc1 <- forecast(m1, h = 24)
fc2 <- forecast(m2, h = 24)

# 准确率指标
accuracy(fc1, test)[2, c("RMSE", "MAE", "MAPE")]
    RMSE      MAE     MAPE 
74.25224 68.57729 14.92756 
accuracy(fc2, test)[2, c("RMSE", "MAE", "MAPE")]
    RMSE      MAE     MAPE 
72.54791 63.21297 13.30345
Note

常用评估指标：

  • RMSE：均方根误差（对大误差敏感）
  • MAE：平均绝对误差
  • MAPE：平均绝对百分比误差（可解释性好）

实战：预测月度销售

# 模拟零售数据
set.seed(42)
sales <- ts(
  100 + 1:60 * 2 +                    # 上升趋势
  30 * sin(2 * pi * 1:60 / 12) +      # 季节性
  rnorm(60, sd = 10),                 # 噪声
  start = c(2020, 1), frequency = 12
)

# 一行完成：建模 + 预测 + 可视化
sales |> 
  auto.arima() |> 
  forecast(h = 12) |> 
  autoplot() +
  theme_minimal() +
  labs(title = "月度销售额预测", x = "年份", y = "销售额")

总结

方法 适用场景 函数
STL分解 理解数据结构 stl()
ARIMA 通用预测 auto.arima()
SARIMA 强季节性数据 auto.arima(seasonal=TRUE)
ETS 短期预测、平滑 ets()
Tip

实践建议：

  1. 先可视化，理解数据特征
  2. 检验平稳性，必要时差分
  3. 对比多个模型，选择最优
  4. 关注置信区间，预测有不确定性